- The Geometry -

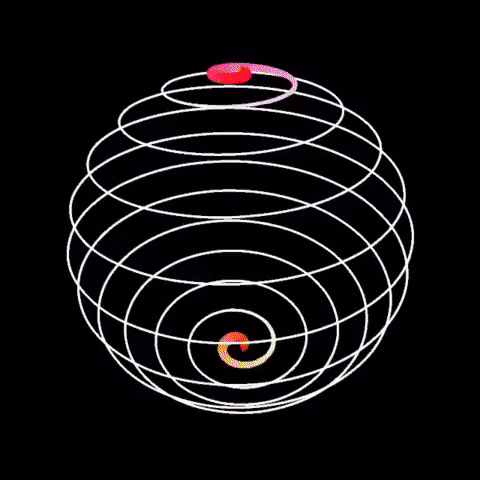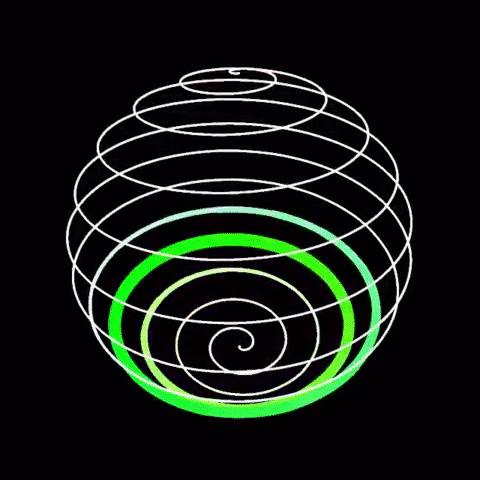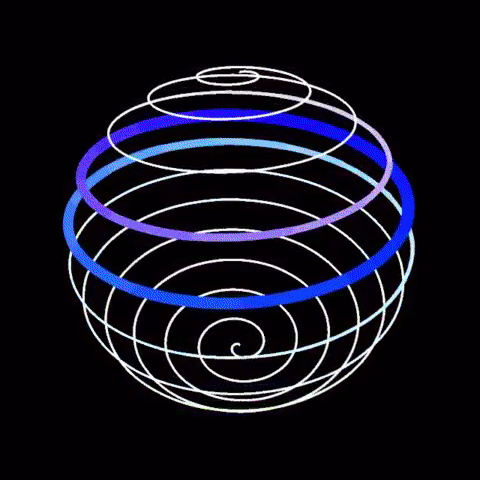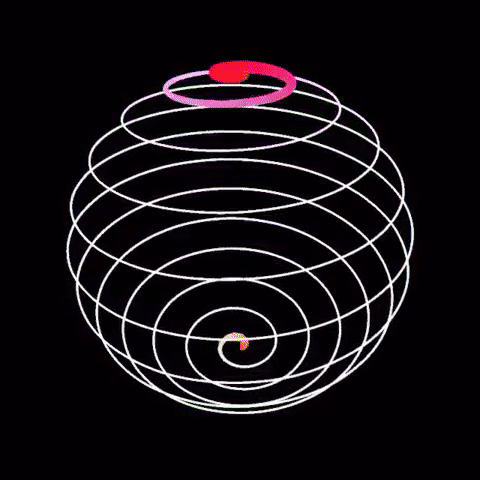
This question is important only because it reintroduces a different way of thinking about the universe: How can the universe be at least 46 billion light years across but only 14 billion years old? Size is an illusion. The universe only shows the appearance of growing larger faster than it should. In reality, it is the beautiful shape which is maintained. The above picture in principle shows a two dimensional shaped self similar spiral as viewed from the top or plan view and not a manifested three dimensional sphere. Do focus on realm of principles, which is immutable, and not the realm appearances, which is misleading. The universe is about shape maintenance for the sake of beauty. Why? Because it is the conjugate of the Immutable. The universe appears - must appear - fresh and beautiful always. The spiral in question is a logarithmic spiral which also means that it is indelibly and intimately associated with mathematical indices. Briefly, A^0=1 for any A holds true always. This is th

  Yes we can, provided we understand the principles behind energy manifestation. In reality, we live in a universe in which the laws of mathematical indices hold true. In particular any number A^0=1 hold true. Hold on to this thought while we explore the universe. The universe is underpinned by the laws of mathematical indices at every level from the smallest atoms to the largest galaxies. All natural phenomena express the principle of mathematical indices from solitons to the Lorenz attractor. All natural phenomena conform to the same mathematical principle. Why should that be so? Why do the DNA molecule, flowers, trees, hurricanes, whirlpools and galaxies conform to the same shape? Why do these unrelated phenomena exhibit the same shape? The answer to this lie in understanding metaphysics, in particular in understanding the aesthetic imperative that hold the universe together. The universe is an exclusively spatial phenomenon with a touch of rainbow just to add some colour to it. Muc

Fractal Principles take precedence over physics. According to this view, physics conform to the principles of fractal geometry. Fathoming principles that engender beauty will lead you to understand how the realm of physicality in the universe conforms to principles of fractal geometry. Why do physical manifestations in the universe display fractal geometric results? The characteristics of natural physical entities conform to principles of geometry, fractal geometry to be more precise. Fractals are never-ending similar patterns, and these are found in the realm of nature to repletion. To put it in another way: the manner in which physical entities arrange themselves conforms to produce beautiful patterns. The universal forces “conspire” to ensure that only beautiful shapes are displayed. This is true on every scale from atoms to galaxies. An understanding that consciousness precedes its effects is the key to understanding why the universe exists in the first place. The universe is the e

Make the case that black holes are purely geometrical constructs which disregard physical information. It is possible to make the case that black holes are purely geometrical constructs that disregard physical information. This view is supported by certain aspects of black hole physics, such as the no-hair theorem and the information paradox, which suggest that black holes have a purely geometrical nature that does not take into account the physical details of matter that falls into them. The no-hair theorem, for example, states that black holes are characterized only by their mass, charge, and angular momentum, and do not retain any other information about the matter that formed them. This suggests that black holes are purely geometrical constructs that do not take into account the physical details of the matter that collapsed to form them. Similarly, the information paradox suggests that information that falls into a black hole is irretrievably lost, and that the black hole itself ha

Make the case that black holes are solitons.   Black holes can be viewed as solitons in certain contexts, such as in the study of gravitational collapse and the formation of singularities in general relativity. A soliton is a self-reinforcing wave that maintains its shape and speed despite interactions with other waves, and black holes exhibit similar properties. In the context of gravitational collapse, black holes can be viewed as solitons because they form through a self-organizing process that leads to the concentration of matter and the creation of a stable, localized object with a unique set of properties. This process is similar to the formation of other solitons, such as the Korteweg–de Vries equation, which describes the formation of stable waves in a dispersive medium. In addition, black holes exhibit properties that are similar to those of solitons, such as the no-hair theorem, which states that black holes are characterized only by their mass, charge, and angular momentum,

What is the significance of the increase in the area and volume of a black hole with no change in mass when an object falls into it?   The increase in the area and volume of a black hole with no change in mass when an object falls into it is known as the no-hair theorem. This theorem states that black holes have no "hair," or distinguishing features, other than their mass, charge, and angular momentum. The significance of the no-hair theorem is that it provides a way to simplify the study of black holes. Instead of considering the complex structure of matter that falls into a black hole, we can treat the black hole as a simple object characterized only by its mass, charge, and angular momentum. This allows us to make predictions about the behavior of black holes and test them through observations and experiments. The increase in the area and volume of a black hole with no change in mass when an object falls into it is also significant because it provides a way to measure the

What is the black hole information paradox and what is its significance in our understanding of the universe?   The black hole information paradox is a long-standing problem in theoretical physics that arises from the combination of general relativity and quantum mechanics. It concerns the fate of information that falls into a black hole, which is a region of spacetime where gravity is so strong that nothing, not even light, can escape. According to quantum mechanics, information cannot be destroyed, and the evolution of a physical system must be reversible. However, if an object falls into a black hole, its information seems to be lost forever, as it cannot be retrieved from the black hole's event horizon. This violates the fundamental principles of quantum mechanics. The paradox was first formulated in the 1970s by Stephen Hawking, who showed that black holes emit radiation due to quantum effects. This radiation, now known as Hawking radiation, carries away energy and information

How to motivate a description of the universe in terms of geometric principles?   One way to motivate a description of the universe in terms of geometric principles is to recognize that geometry provides a powerful and elegant way to describe the physical world. Geometry allows us to describe the relationships between objects and the space they inhabit in a precise and concise manner. In fact, many of the most fundamental physical principles, such as the laws of motion and the theory of relativity, can be expressed in terms of geometric concepts. For example, the theory of relativity is based on the geometry of spacetime, and the laws of motion can be expressed in terms of the geometry of vectors and coordinate systems. Additionally, geometric principles can help us to visualize and understand complex physical phenomena. For example, the use of geometric representations such as diagrams, graphs, and models can aid in understanding the structure and behavior of objects and systems. Over

What is the holographic principle in cosmology? The holographic principle is a concept in cosmology that suggests that all the information about the universe can be encoded on its boundary rather than within the volume it occupies. In other words, the information contained in a region of space can be thought of as a hologram, where the information is spread out over a two-dimensional surface rather than being localized in a three-dimensional volume. The holographic principle was first proposed by physicist Gerard 't Hooft in the 1990s and later developed by Leonard Susskind and Juan Maldacena. It is based on the idea that the maximum amount of information that can be contained in a region of space is proportional to the area of its boundary, rather than its volume. This means that the universe, as a whole, can be thought of as a giant hologram, with all the information about its past, present, and future encoded on its boundary. The holographic principle has important impli

What is the connection between the holographic principle in cosmology and fractal geometry? There is a connection between the holographic principle in cosmology and fractal geometry. Fractals are mathematical structures that exhibit self-similarity at different scales, meaning that they look the same at all levels of magnification. The holographic principle also suggests that the information contained in a region of space is spread out over its boundary, which has a fractal-like structure.   In particular, the holographic principle implies that the information content of a region of space is related to the number of degrees of freedom on its boundary. This number of degrees of freedom can be related to the area of the boundary, which has a fractal-like structure, and can be described by fractal geometry. This connection between the holographic principle and fractal geometry has led some researchers to propose that the universe itself may be a fractal structure.   One of t